Статья опубликована в рамках: XXXI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 28 апреля 2015 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
ПРИМЕНЕНИЕ РЯДА ФУРЬЕ В НЕФТЕГАЗОВОМ ДЕЛЕ
Галиев Раиль Рустемович
студент 1 курса ВПО ОФ УГНТУ, РФ, г. Октябрьский
Е-mail : yamakasi_1996_1996@mail.ru
Шияпов Айнур Ахатович
студент 1 курса ВПО ОФ УГНТУ, РФ, г. Октябрьский
Е-mail : NooRick96@mail.ru
Габдрахманова Клара Фаткуллиновна
научный руководитель, канд. техн. наук, доцент кафедры ИТМЕН, ВПО ОФ УГНТУ, РФ, г. Октябрьский
В данной статье рассматриваются возможности применения рядов Фурье в нефтегазовом деле. Особое внимание уделено изучению особенностей решения задач с помощью рядов Фурье, а именно на примере статически неопределимой балки.
В данной статьи рассматриваются теоретические подходы и определения ряда Фурье. Рассматриваются основные определения и способы вычисления ряда, а также коэффициентов ряда Фурье. Основное внимание уделено разложению функций в ряде Фурье по косинусам и синусам, и определения четности и нечетности. И рассмотрели равномерную сходимость ряда Фурье.
Введение
В наше время математика стала широко использоваться на практике. Любой производственный или технологический процесс не может обойти стороной основные математические закономерности. Эффективность применения математического моделирования для различных инструментов позволяет рассчитывать различные устройства и агрегаты, способные выполнять операции с большой точностью и помогают проводить сложные расчеты и вычисления при проектировании различных сооружений, производить необходимые расчеты при геодезических исследованиях с большой точностью.
Элементы математики на производстве можно встретить практически на каждом шагу и поэтому специалистам важно знать методы анализа и расчета. Например, специалисту в нефтегазовом деле при инженерно-технических расчетах и исследованиях при рассмотрении ряда задач измерительной техники, а также при анализе результатов измерений нестационарных параметров. Ряды Фурье допускают проводить такие расчеты.
Давайте теперь вместе обратимся к теории рядов Фурье, ближе познакомимся с формулами и определениями, необходимые для решения задачи.
Тригонометрический ряд :
![]() (1)
(1)
с коэффициентами, называемые коэффициенты Фурье , определяемые по формулам(2), (3), (4):
 (2)
(2)
![]() (3)
(3)
 (4)
(4)
называется рядом Фурье функции f(x).
Разложения функций в ряд Фурье по косинусам :
 (5)
(5)
где коэффициенты ряда Фурье вычисляются по формулам (6), (7):
 (6)
(6)
 (7)
(7)
Разложение функции в ряд Фурье по синусам :

где коэффициенты ряда Фурье вычисляются по формулам (8):
 (8)
(8)
Важно отметить, что функция f(x) с периодом 2 содержащая только синусы или косинусы называется нечетной или четной периодической функцией соответственно.
Равномерная сходимость ряда Фурье.
Принято считать, что последовательное значение сумм ряда Фурье {fn (x)} равномерно сходится к функции f (x) (рисунок 1):
![]() (9)
(9)
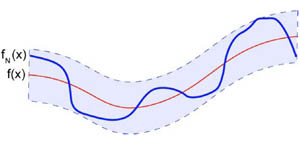
Рисунок 1.
Пример:
Пусть на балку длиной ![]() , действует некая сила; закрепим эту балку так, чтобы ее вертикальные сдвиги и изгибающие моменты на концах балки были равны нулю:
, действует некая сила; закрепим эту балку так, чтобы ее вертикальные сдвиги и изгибающие моменты на концах балки были равны нулю:
![]() . (1)
. (1)
Функцию прогиба ![]() представим рядом Фурье. Так как в данной функции изгибающий момент
представим рядом Фурье. Так как в данной функции изгибающий момент![]() и функция прогиба
и функция прогиба ![]() — нечетные функции
— нечетные функции ![]() . Поэтому будем раскладывать эти функции на отрезке
. Поэтому будем раскладывать эти функции на отрезке ![]() . Ряд Фурье этой функции по синусам будет иметь вид:
. Ряд Фурье этой функции по синусам будет иметь вид:
 . (2)
. (2)
Аналогично разложим изгибающий момент ![]() .
.
 . (3)
. (3)
Пусть![]() — нагрузка, которая в любой точке
— нагрузка, которая в любой точке ![]() балки порождает изгибающий момент.
балки порождает изгибающий момент.
Продифференцировав ряд (2) и подставив полученное с рядом (3), получаем равенство двух рядов Фурье, из этого равенства, приравниваем коэффициенты, стоящие при ![]()
![]() в левой и правой частях и получаем:
в левой и правой частях и получаем:
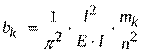
![]() . (4)
. (4)
Исходя из формулы (4) функции прогиба будет иметь вид:
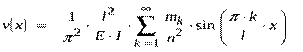 . (5)
. (5)
Причем коэффициенты ![]() определяются по формуле (3).
определяются по формуле (3).
Благодаря данному методу, можем рассчитать следующие параметры:
• в случае сосредоточенной нагрузки:
 ;(6)
;(6)
 ;(7)
;(7)
• в случае сосредоточенного момента:
 ;(8)
;(8)
 .(9)
.(9)
На основаниях полученных результатов рассмотрим статически неопределимую задачу. Пусть балка длины ![]() закреплена левым концом, а правым находится на шарнирно-подвижной опоре, на балку посередине действует вертикальная сила
закреплена левым концом, а правым находится на шарнирно-подвижной опоре, на балку посередине действует вертикальная сила ![]() , направленная вниз (см. рис. 2).
, направленная вниз (см. рис. 2).

Рисунок 2.
В этой статически неопределимой задаче можем заметить что: равновесие балки не нарушается, если одну из четырех связей отбросить, введя в жесткой заделке шарнир.
Значит согласно (7) угол поворота сечения балки в точке ![]() под действием силы
под действием силы![]() будет равен:
будет равен:
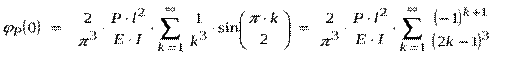 .(10)
.(10)
Если в точке ![]() к этой балке приложить сосредоточенный изгибающий момент
к этой балке приложить сосредоточенный изгибающий момент ![]() , то, исходя из (9), угол поворота сечения в точке
, то, исходя из (9), угол поворота сечения в точке ![]() под действием этого момента будет равен:
под действием этого момента будет равен:
 (11).
(11).
Так как балка закреплена одним концом, то имеем:
![]() (12).
(12).
Подставляя равенства (10) и (11) в выражение (12), получим:
 (13).
(13).
После суммирования рядов стоящих в (13):
 ;
;  .
.
Окончательно получаем:
 (14).
(14).
Если сложить функцию прогиба ![]() балки с моментом
балки с моментом ![]() и функцию прогиба
и функцию прогиба ![]() , то можно найти значение функции прогиба
, то можно найти значение функции прогиба ![]() балки.
балки.
Используя выражение (14) и формулы (6), (7) для момента ![]() , то можно получить:
, то можно получить:

 . (15)
. (15)
Продифференцировав ряд (15), из уравнения (3) можно найти изгибающий момент ![]() , который будет равен:
, который будет равен:
 . (16)
. (16)
Надо отметить, что ряд Фурье (16) функции ![]() сходится к
сходится к ![]() только в точках ее непрерывности на промежутке разложения, т. е. в этом случае на промежутке
только в точках ее непрерывности на промежутке разложения, т. е. в этом случае на промежутке ![]() ; в точках разрыва и на границах промежутка разложения значения функции
; в точках разрыва и на границах промежутка разложения значения функции![]() и суммы ряда Фурье
и суммы ряда Фурье ![]() могут и не совпадать. Так, у нас в точке
могут и не совпадать. Так, у нас в точке ![]() сумма ряда
сумма ряда ![]() , а значение момента
, а значение момента ![]() .
.
Итак, мы нашли решение одной из статически неопределимых задач изгиба балки с помощью использования не стандартного для таких задач метода разложений в ряд Фурье.
Заключение
В заключение отметим, что ряды Фурье нашли свое применение в нефтегазовом деле, которые позволяют решить важные задачи математической физики. Например, некоторыми из них является задача, изложенная в данной статье,- изгиба балки.
Список литературы:
1.Виленкин Н.Я., Цукерман В.В. Ряды: учебное пособие для студентов-заочников 3-го курса физико-математических факультетов педагогических институтов. Москва: издательство «Просвещение»,1982 г. — 126 C.
2.Зорич В.А. Математический анализ. Часть II. М.: МЦНМО, 2002. — 108—116 C.
3.Ильин В.А., Позняк Э.Г. Основы математического анализа. Часть II.// М.: Наука. Физматлит, 2000. — 16—18 C.
4.Ильин В.А., Садовничий В.А., Сендов Б.Х. Математический анализ.// М.: Наука, 1979. — 95—118 C.
5.Шнейдер В.Е., Слуцкий А.И., Шумов А.С. «Краткий курс высшей математики», том2, М.: «Высшая школа», 1978 г. — 167 С.
отправлен участнику


Комментарии (11)
Оставить комментарий