Статья опубликована в рамках: XXI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 06 августа 2014 г.)
Наука: Математика
Секция: Математическая логика, алгебра и теория чисел
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ГРУППЫ ЧИСЛОВЫХ «СОЗВЕЗДИЙ»
Мамедяров Даглар Мамедярович
канд. пед. Наук, Дербентский филиал «Московский государственный гуманитарный университет им. М.А. Шолохова», Республика Дагестан, г. Дербент
E-mail:
GROUPS OF NUMERICAL “CONSTELLATIONS”
Daglar Mamedyarov
candidate of pedagogic sciences, Derbent Branch of Sholokhov Moscow State University for the Humanities, Russia, Derbent
АННОТАЦИЯ
Группами «числовых созвездий» в свое время занимались два великих академика: Гольдбах и Эйлер. В своей статье автор ставит цель: найти правило для получения аналогичных и других интересных «числовых созвездий». В ходе такой исследовательской работы были найдены способы получения различных групп созвездий с использованием свойств треугольных, пирамидальных и других чисел сочетаний. Материал данной статьи с успехом можно использовать на факультативных и кружковых занятиях.
ABSTRACT
In due time two great academicians Goldbach and Euler used to work with groups of “numerical constellations”. In this article the author’s goal is to find a rule for receiving similar and other interesting “numerical constellations”. During this research the ways of gaining different groups of constellations using properties of triangular, pyramidal and other numbers of combinations have been found. Material of this article could be successfully used in interest groups and extracurricular activities.
Ключевые слова: числовые созвездия; тождества.
Keywords : numerical constellations; identities.
Числа, подобно звездам, можно группировать в разнообразные числовые «созвездия».
«Созвездие» из шести чисел 2, 3, 7, 1, 5, 6 занятно тем, что сумма первых трех чисел равна сумме последних трех, равны даже суммы их квадратов:
![]()
![]()
Эти числа 2, 3, 7, 1, 5, 6 заменяют собой шесть неизвестных ![]() в системе уравнений
в системе уравнений
![]()
Есть бесконечно много других чисел, которые являются решением этой системы. Еще ярче «созвездия» из восьми чисел 0, 5, 5, 10, 1, 2, 8, 9 и из десяти чисел 1, 4, 12, 13, 20, 2, 3, 10, 16, 19. В каждом из них сумма чисел первой половины равна сумме чисел второй половины, затем равны суммы квадратов тех же чисел, больше того, равны даже суммы кубов тех же чисел:


Имеются и другие группы чисел, связанные точно такими же соотношениями, но как подобрать такие числа? В «тайну» всех приведенных здесь «числовых созвездий» первыми проникли еще в 1750—1751 годы два петербургских академика Гольдбах и гениальный Эйлер. Они нашли ряд формул, пригодных для решения в целых числах некоторых систем уравнений, в частности и тех, которые приводят к упомянутым «числовым созвездиям».
Для подбора чисел, образующих первое «созвездие»:
![]()
![]()
оказались пригодными такие формулы:
![]()
и
![]()
Надо заменить в этих формулах буквы ![]() любыми числами, и вы получите сколько угодно чисел первого «созвездия». В частности, при
любыми числами, и вы получите сколько угодно чисел первого «созвездия». В частности, при ![]() получается «созвездие», приведенное в качестве первого примера: 2, 3, 7, 1, 5, 6.
получается «созвездие», приведенное в качестве первого примера: 2, 3, 7, 1, 5, 6.
Эйлер и Гольдбах дали еще и другую группу формул для чисел первого «созвездия».
![]()
![]()
где: ![]() тоже произвольные числа.
тоже произвольные числа.
Для подбора чисел, образующих второе «созвездие»:

пригодны следующие формулы:  [1].
[1].
Занимаясь этой проблемой, мы нашли другие интересные числовые «созвездия» и правила нахождения чисел для таких «созвездий», в частности для первого «созвездия».
На примерах объясним суть нашего правила ![]() .
.
Возьмем разность чисел ![]()
Пусть ![]() имеем:
имеем:
![]()
![]()
![]() и т. д.
и т. д.
Пусть ![]() , имеем:
, имеем:
![]()
![]()
![]() и т. д.
и т. д.
Пусть ![]() , имеем:
, имеем:
![]()
![]()
![]() и т. д.
и т. д.
Если в этих равенствах возьмем разность двух соседних значений, то получим ![]() .
.
Например, при ![]() и т. д.
и т. д.
при ![]() и т. д.
и т. д.
Поэтому, мы можем составлять множество тождеств вида
![]()
![]() и т. д., или
и т. д., или
![]()
![]() и т. д.
и т. д.
Отсюда, используя определение числа сочетаний, получаем
![]() или
или
![]() Имеем:
Имеем:
![]()
![]() или
или ![]() Имеем:
Имеем:
![]()
Найденные нами числа являются решениями системы второго «созвездия», правда, только для первых двух уравнений. Используя такие тождества, можно получить сколько угодно решений для системы
![]()
А как получить числа для первого «созвездия»?
Покажем это на примере.
Воспользуемся равенством
![]() [2].
[2].
Пусть ![]()
Имеем: ![]() Возьмем следующее равенство, где
Возьмем следующее равенство, где ![]()
Отсюда ![]() или
или
![]()
Пусть ![]()
Имеем: ![]() Возьмем второе равенство, где
Возьмем второе равенство, где
![]() Тогда
Тогда ![]()
Приравнивая обе части, получаем:
![]() или
или
![]()
![]() .
.
Общее правило такое: из тождества ![]() взяв вместо
взяв вместо ![]() и
и ![]() произвольные числа, вычисляем первое тождество. Так как равенство не зависит от выбора
произвольные числа, вычисляем первое тождество. Так как равенство не зависит от выбора ![]() , то вычисляем второе тождество, такое, чтобы его меньший член совпадал со старшим членом первого тождества. То есть складываем к старшему члену первого тождества
, то вычисляем второе тождество, такое, чтобы его меньший член совпадал со старшим членом первого тождества. То есть складываем к старшему члену первого тождества ![]() .
.
Тождество ![]() всегда приводит к решению системы:
всегда приводит к решению системы:
![]()
Приведем один пример:
![]() Отсюда
Отсюда
![]()
![]()
Приведем несколько другие интересные «созвездия».
Вычислим разность треугольных чисел вида ![]() . Например,
. Например,
![]()
![]() и т. д.
и т. д.
Получаем ![]() и т. д.
и т. д.
Число 4 запишем в виде ![]() по формуле
по формуле ![]()
Имеем: ![]() или
или ![]()
Используя определение числа сочетаний, имеем:
![]()
![]()
Получаем систему
![]()
![]() ,
, ![]()
Отсюда
![]()
Используя определение числа сочетаний, получаем:
![]() или
или
![]() . Имеем систему
. Имеем систему
![]()
Используя такие тождества можно получить бесконечное множество решений системы
![]()
Для получения таких равенств можно использовать равенство
![]()
Пусть ![]() . Составим равенства
. Составим равенства
![]()
![]()
![]() и т .д.
и т .д.
Найдем разность двух соседних тождеств.
1. ![]() но
но ![]() есть
есть ![]() Отсюда
Отсюда
![]() имеем
имеем
![]()
2. ![]() или
или ![]() Имеем:
Имеем:
![]()
Используя разности ![]() при
при ![]() можно получить сколько угодно такие «созвездия». Можно получить и другие «созвездия», подобные
можно получить сколько угодно такие «созвездия». Можно получить и другие «созвездия», подобные ![]() или
или ![]() которые являются решениями системы
которые являются решениями системы
![]()
Если возьмем разности ![]() и составим равенства
и составим равенства ![]() , получаем
, получаем ![]()
Используя определения числа сочетаний, получаем решения системы

Пример 1 . ![]() или
или
![]() или
или
![]()
![]() имеем
имеем
![]()
Пример 2 . ![]() или
или
![]()
Имеем: ![]()
![]()
![]()
Если возьмем разности чисел вида ![]() , получим решение системы
, получим решение системы

Приведем несколько примеров.
Пример 1 . ![]() Отсюда
Отсюда
![]()
Имеем: ![]()
![]()
Пример 2 . ![]() или
или
![]() Отсюда
Отсюда
![]()
![]()
Из наших примеров можно сделать вывод: если взять равенства вида ![]() , то записывая
, то записывая ![]() в виде
в виде ![]() можно находить решения системы уравнений вида
можно находить решения системы уравнений вида ![]() , где
, где ![]() разность
разность ![]() .
.
Приведем примеры:
1. ![]()
Отсюда ![]() . Используя определение числа сочетаний, имеем
. Используя определение числа сочетаний, имеем ![]()
Имеем: ![]()
2. ![]()
![]()
![]()
![]()
3. ![]()
![]()
![]()
![]()
4. ![]()
![]()
![]()
![]()
Составляя разнообразные комбинации из чисел сочетаний, можно получать различные числовые «созвездия».
Составим различные числовые «созвездия».
Возьмем выражение ![]() Отсюда
Отсюда
![]() Далее
Далее
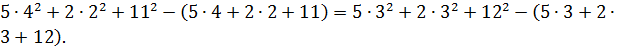 Имеем:
Имеем:
![]()
Из ![]() , получаем
, получаем
![]() Имеем:
Имеем:
 Отсюда
Отсюда
![]() или
или
![]()
Возьмем ![]() Отсюда
Отсюда
![]() Имеем
Имеем
 Отсюда
Отсюда
![]()
Из ![]() мы получили решение системы
мы получили решение системы

Из ![]() получили решение системы
получили решение системы

Из ![]() получили решение системы
получили решение системы
![]()
Из равенства ![]() имеем:
имеем:
![]() или
или
![]()
![]() , получили решение системы
, получили решение системы
![]()
Возьмем такое выражение ![]()
Отсюда ![]()
Имеем:  или
или
![]()
Получили решение системы
![]()
Замечание : если записать эти тождества в общем виде и придавать им различные значения, мы получим множество решений полученных систем.
Рассмотрим еще одно «созвездие». Оно представляет собой систему
![]()
Прежде чем приведем решение данной системы, остановимся на одном историческом факте.
Индийский студент Сундарам в 1934 году придумал следующую таблицу:
4, 7, 10, 13, 16, 19, 22, 25, 28, …
7, 12, 17, 22, 27, 32, 37, 42, 47, …
10, 17, 24, 31, 38, 45, 52, 59, 66, …
13, 22, 31, 40, 49, 58, 87, 96, 105, …
…
Если взять число, которое не входит в эту таблицу, умножить на 2 и прибавить 1, то получится всегда простое число. Например, 15 не входит в эту таблицу. ![]() простое.
простое.
Заметим, что любой член первой строки имеет вид ![]() , второй —
, второй — ![]() третьей —
третьей — ![]() четвертой —
четвертой — ![]() и т. д. То есть каждая трока представляет арифметическую прогрессию с разностью
и т. д. То есть каждая трока представляет арифметическую прогрессию с разностью ![]() .
.
Каждый член таблицы Сундарама можно записать в виде ![]() . Например,
. Например, ![]() и т. д.
и т. д.
![]() и т. д.
и т. д.
Заметьте, что в каждой арифметической прогрессии есть одинаковые члены. Например, ![]()
Для любых нечетных чисел ![]() и
и ![]() можно находить такие тождества, т. е. для любой арифметической прогрессии с разностями
можно находить такие тождества, т. е. для любой арифметической прогрессии с разностями ![]() и
и ![]() можно найти общий член.
можно найти общий член.
Приведем пример.
Пусть ![]() . Найдем общие члены этих прогрессий, сравнивая формулы общих членов
. Найдем общие члены этих прогрессий, сравнивая формулы общих членов ![]()
Пусть ![]() , тогда
, тогда ![]() или
или ![]() , тогда
, тогда ![]() .
.
То есть при ![]()
Эти прогрессии имеют равные члены.
Возьмем равенство ![]()
Отсюда ![]() или
или ![]()
Используя определение числа сочетаний, имеем:
![]() Отсюда имеем
Отсюда имеем ![]()
Возьмем равенство ![]()
Отсюда ![]() или
или ![]() Имеем:
Имеем:
![]()
Получаем систему ![]()
Возьмем равенство ![]()
Отсюда ![]() или
или ![]() Имеем:
Имеем:
![]()
Получаем систему ![]()
Таким образом, мы можем найти бесконечное множество решений системы ![]()
Решение системы ![]()
Для нахождения решения нашей системы можно использовать различные комбинации из треугольных чисел.
Приведем несколько примеров.
1. ![]()
Приравнивая левые части, получаем ![]() . Отсюда
. Отсюда
![]() или
или ![]() . Имеем:
. Имеем:
![]()
Получаем систему ![]()
2. ![]()
Отсюда ![]() или
или ![]()
![]() . Имеем:
. Имеем:
![]()
Получаем систему ![]()
3. Возьмем ![]()
Отсюда ![]() Имеем:
Имеем: ![]() или
или
![]() .
.
![]()
Получаем систему ![]()
Как найти решения этой системы в натуральных числах мы уже показали при решении уравнения ![]() . в этом равенстве равны основания, т. е.
. в этом равенстве равны основания, т. е. ![]()
Решение системы 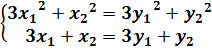
Воспользуемся равенством ![]() . Это равенство верно для любых
. Это равенство верно для любых ![]() .
.
Например,  и т. д.
и т. д.
Имеем: ![]()
Отсюда ![]() или
или ![]()
Имеем: ![]() .
.
Получаем систему ![]()
Из ![]() имеем:
имеем: ![]()
Отсюда получаем: ![]() .
.
Имеем систему: ![]()
Решение системы ![]()
Воспользуемся равенством ![]() . Это равенство верно при любых
. Это равенство верно при любых ![]() .
.
Возьмем два равенства ![]() Отсюда
Отсюда
![]() Имеем:
Имеем:
![]() .
.
Получаем систему ![]()
Приведем другой пример.
Возьмем равенство ![]() Имеем:
Имеем:
![]() .
.
Получаем: ![]()
Возьмем равенство ![]()
Имеем: ![]() Далее
Далее
![]() .
.
Получаем: ![]()
Таким образом, мы можем находить бесконечное множество решений данной системы.
Решение системы ![]()
Покажем решение на примерах.
Возьмем равенство ![]()
Отсюда ![]() или
или ![]()
Далее ![]() .
.
Имеем систему ![]()
Решение системы 
Воспользуемся равенством вида ![]() .
.
Например, ![]()
Отсюда ![]()
Далее ![]() Имеем:
Имеем:
![]() .
.
Получаем систему ![]()
Возьмем равенство ![]()
Отсюда ![]() или
или
![]() Имеем:
Имеем:
![]() .
.
Получаем систему ![]()
Решение системы ![]()
1. Возьмем равенство ![]()
Отсюда ![]() Имеем:
Имеем:
 .
.
Получаем систему ![]()
Заметим, что эти числа удовлетворяют и уравнению
![]() , т. е.
, т. е.
![]() ,
,
![]() , т. е. мы нашли решение системы:
, т. е. мы нашли решение системы:
 (*)
(*)
2. Возьмем ![]()
Отсюда ![]()
Имеем:  .
.
Получаем систему
![]()
Проверим, удовлетворяют ли эти числа уравнению
![]() ?
?
![]()
![]()
Убедились, что эти числа являются решением системы (*). Используя такие тождества мы можем находить бесконечное множество решений системы (*).
Решение системы 
Воспользуемся равенством ![]() .
.
Возьмем равенство ![]()
Отсюда ![]() или
или
![]() .
.
Используя формулу ![]() получаем
получаем
![]() .
.
Получаем систему ![]() но эти числа удовлетворяют и уравнению
но эти числа удовлетворяют и уравнению ![]() , т. е.
, т. е.
![]() ,
, ![]() .
.
Используя тождество ![]() , при различных значениях
, при различных значениях ![]() можно находить решения системы уравнений от первой до
можно находить решения системы уравнений от первой до ![]() й степени с биноминальными коэффициентами разложения бинома Ньютона
й степени с биноминальными коэффициентами разложения бинома Ньютона ![]() й степени.
й степени.
Например, из тождеств
![]() =1 и
=1 и
![]() =1 можно получить системы уравнений.
=1 можно получить системы уравнений.

Из тождества
![]()
![]() .
.
Имеем;

Это одно из решений. Такие системы имеют бесконечное множество решений.
Список литературы:
1.Кордемский Б.А. Математическая смекалка. Москва 1965 г. — Стр. 336.
2.Мамедяров Д.М., Вакилов Ш.М. Некоторые свойства соединений и фигурных чисел и их применение при решении задач. Дербент 2006 г. — Стр. 68.
3.Мамедяров Д.М. Неопределенные уравнения и их системы. Дербент 2013. Стр.241.
4.Мамедяров Д.М. Вакилов Ш.М. Как научить учащихся маленьким открытиям. Международная научно-практическая конференция. Материалы конференции 24,26 июня 2011 года. Дербент 2011.
дипломов


Комментарии (1)
Оставить комментарий